CS180 Project #2: Fun with Filters and Frequencies!

Part 1: Fun with Filters

Part 1.1: Finite Difference Operator

Apply the humble finite difference as the filter in the x and y directions:

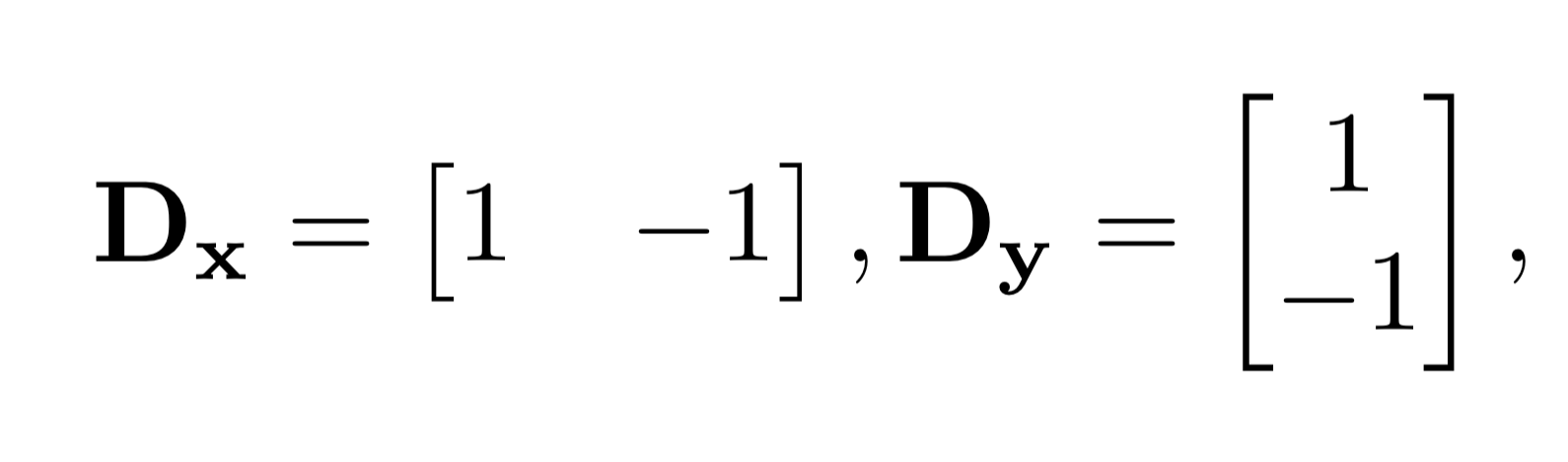
Approximate the partial derivatives by: \( \left[ -1 \quad 1 \right] \; \text{to estimate} \; \frac{\partial f(x, y)}{\partial x} \approx \frac{f(x + 1, y) - f(x, y)}{1} \), \( \left[ -1 \quad 1 \right]^\top \; \text{to estimate} \; \frac{\partial f(x, y)}{\partial x} \approx \frac{f(x, y+1) - f(x, y)}{1} \).

The gradient magnitude is given by: \( ||\delta f|| = \sqrt{\frac{\partial f}{\partial x}^2 + \frac{\partial f}{\partial y}^2} \).

Here the finite different operator is applied to covolved with input image to produce the partial derivatives. Then the gradient magnitude is computed by the formula.

Part 1.2: Derivative of Gaussian (DoG) Filter

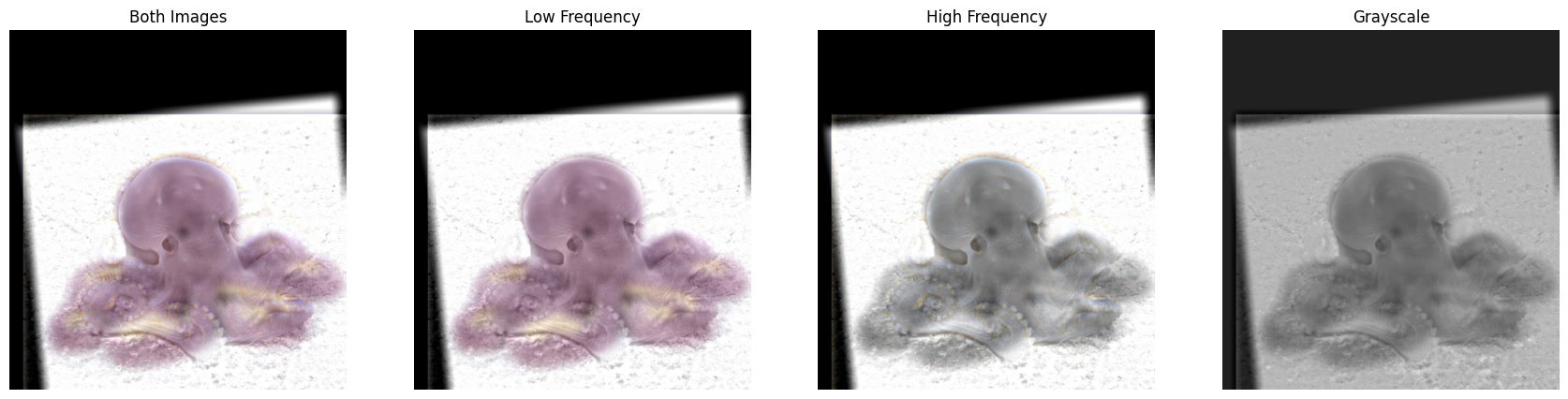
Blur the image by Gaussian Filter before applying the finite difference operators, the visualizations have less noise and the edges are clearer:

By the commutativity and associativity of convolution, apply the Gaussian Filter convolved by finite difference operators to the images directly should produce the same result:

Part 2: Fun with Frequencies!

Part 2.1: Image "Sharpening"

Apply the unsharp mask filter to the following sample images:

After blurring the images, applying the unsharp mask filter will emphasize the edges of general shapes instead of details since the noise is filtered before sharpening:

Part 2.2: Hybrid Images

Bells & Whistles: It works better with color from both images.

The log magnitude of the Fourier transform of the hybrid of casper octopus and octopus plushie:

Part 2.3: Gaussian and Laplacian Stacks

Apply the Gaussian and Laplacian stacks to the Oraple:

Part 2.4: Multiresolution Blending (a.k.a. the oraple!)

Apply the Gaussian and Laplacian stacks to the Oraple: